1. Giới hạn (Limits)
1.1. Định nghĩa
Gọi $f$ là hàm số được xác định trên khoảng mở chứa $c$ (trừ tại $c$) và $L$ là số thực. Khi đó: $\lim\limits_{x \to c} f\left( x \right) = L$ có nghĩa là với mỗi $\varepsilon > 0$ sẽ $\exists \delta > 0$ sao cho nếu $0 < \left| {x - c} \right| < \delta $ thì $\left| {f\left( x \right) - L} \right| < \varepsilon $
Giới hạn hàm số $f$ khi $x \to c$
Ví dụ: Cho giới hạn $\mathop {\lim }\limits_{x \to 3} \left( {2x - 5} \right) = 1$, tìm $\delta$ sao cho $\left| {\left( {2x - 5} \right) - 1} \right| < 0,01$ khi $0 < \left| {x - 3} \right| < \delta $.
Giải:
Để tìm $\delta$ ta cần tìm mối quan hệ giữa $\left| {\left( {2x - 5} \right) - 1} \right|$ và $\left| {x - 3} \right|$.
Ta có: $\left| {\left( {2x - 5} \right) - 1} \right| < 0,01 \Leftrightarrow \left| {2x - 6} \right| < 0,01 \Leftrightarrow \left| {x - 3} \right| < 0,005$.
$ \Rightarrow \delta = 0,005$
Ví dụ: Sử dụng định nghĩa để chứng minh rằng: $\mathop {\lim }\limits_{x \to 2} \left( {3x - 2} \right) = 4$.
Giải:
Ta cần tìm mối quan hệ giữa $\left| {\left( {3x - 2} \right) - 4} \right|$ và $\left| {x - 2} \right|$.
Ta có: $\left| {\left( {3x - 2} \right) - 4} \right| = 3\left| {x - 2} \right|$
Chọn $\delta = \dfrac{\varepsilon }{3}$ vì $0 < \left| {x - 2} \right| < \delta = \dfrac{\varepsilon }{3}$ $ \Rightarrow \left| {\left( {3x - 2} \right) - 4} \right| = 3\left| {x - 2} \right| < 3\left( {\dfrac{\varepsilon }{3}} \right) = \varepsilon $
Ví dụ: Sử dụng định nghĩa để chứng minh rằng: $\mathop {\lim }\limits_{x \to 2} {x^2} = 4$.
Giải:
Ta cần tìm mối quan hệ giữa $\left| {{x^2} - 4} \right|$ và $\left| {x - 2} \right|$.
Ta có: $\left| {{x^2} - 4} \right| = \left| {x + 2} \right|\left| {x - 2} \right|$.
Với $\forall x \in \left( {1,3} \right)$, ta có $x + 2 < 5 \Rightarrow \left| {x + 2} \right| < 5$.
Gọi $\delta = \min \left( {\dfrac{\varepsilon }{5},1} \right)$, khi $0 < \left| {x - 2} \right| < \delta $, ta có: $$\left| {{x^2} - 4} \right| = \left| {x + 2} \right|\left| {x - 2} \right| < 5\left( {\dfrac{\varepsilon }{5}} \right) = \varepsilon $$
1.2. Tính giới hạn
1.2.1. Tính chất
Các giới hạn cơ bảnGọi $b$ và $c$ là các số thực và $n$ là số nguyên dương.
- $\mathop {\lim }\limits_{x \to c} b = b$
- $\mathop {\lim }\limits_{x \to c} x = c$
- $\mathop {\lim }\limits_{x \to c} {x^n} = {c^n}$
Gọi $b$ và $c$ là các số thực và $n$ là số nguyên dương, và gọi $f$ và $g$ là các hàm số với các giới hạn $\mathop {\lim }\limits_{x \to c} f\left( x \right) = L$ và $\mathop {\lim }\limits_{x \to c} g\left( x \right) = K$.
- $\mathop {\lim }\limits_{x \to c} \left[ {bf\left( x \right)} \right] = bL$
- $\mathop {\lim }\limits_{x \to c} \left[ {f\left( x \right) \pm g\left( x \right)} \right] = L \pm K$
- $\mathop {\lim }\limits_{x \to c} \left[ {f\left( x \right)g\left( x \right)} \right] = LK$ \item[+] $\mathop {\lim }\limits_{x \to c} \left[ {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}} \right] = \dfrac{L}{K},K \neq 0$
- $\mathop {\lim }\limits_{x \to c} {\left[ {f\left( x \right)} \right]^n} = {L^n}$
Ví dụ: Chứng minh $\mathop {\lim }\limits_{x \to + \infty } \sin x$ không tồn tại.
Giải:
Để chứng minh giới hạn này không tồn tại, ta sử dụng giới hạn của dãy số.
Ta chọn 2 dãy số bất kì tiến về vô cực: ${u_n} = n\pi $ và ${u_n} = \dfrac{\pi }{2} + 2n\pi $ với $n$ là số nguyên dương.
Với dãy số ${u_n} = n\pi $, ta có: $\mathop {\lim }\limits_{n \to + \infty } \sin n\pi = 0$ và với dãy số ${u_n} = \dfrac{\pi }{2} + 2n\pi $, ta có: $\mathop {\lim }\limits_{n \to + \infty } \sin \left( {\dfrac{\pi }{2} + 2n\pi } \right) = 1$.
Do đó, $\mathop {\lim }\limits_{x \to + \infty } \sin x$ không tồn tại.
Giới hạn của hàm đa thức và hàm phân thức
Nếu $p$ là hàm đa thức và $c$ là một số thực thì \begin{equation} \mathop {\lim }\limits_{x \to c} \left[ {p\left( x \right)} \right] = p\left( c \right) \end{equation} Nếu $r$ là hàm phân thức $r\left( x \right) = \dfrac{{p\left( x \right)}}{{q\left( x \right)}}$ và $c$ là một số thực sao cho $q\left( c \right) \neq 0$ thì \begin{equation} \mathop {\lim }\limits_{x \to c} \left[ {r\left( x \right)} \right] = r\left( c \right) = \frac{{p\left( c \right)}}{{q\left( c \right)}} \end{equation}
Giới hạn của hàm chứa một căn
Gọi $n$ là một số nguyên dương. \begin{equation} \mathop {\lim }\limits_{x \to c} \sqrt[n]{x} = \sqrt[n]{c} \end{equation} (nếu $n$ là số chẵn thì $c > 0$)
Giới hạn của hàm hợp
Nếu $f$ và $g$ là các hàm số sao cho $\mathop {\lim }\limits_{x \to c} g\left( x \right) = L$ và $\mathop {\lim }\limits_{x \to L} f\left( x \right) = f\left( L \right)$ thì \begin{equation} \mathop {\lim }\limits_{x \to c} f\left( {g\left( x \right)} \right) = f\left( {\mathop {\lim }\limits_{x \to c} g\left( x \right)} \right) = f\left( L \right) \end{equation}
1.2.2. Kĩ thuật tính giới hạn
Gọi $c$ là một số thực và $f\left( x \right) = g\left( x \right)$ với $\forall x \neq c$ trong khoảng mở chứa $c$. Nếu $\mathop {\lim }\limits_{x \to c} g\left( x \right)$ tồn tại thì $\mathop {\lim }\limits_{x \to c} f\left( x \right)$ cũng tồn tại và $\mathop {\lim }\limits_{x \to c} f\left( x \right) = \mathop {\lim }\limits_{x \to c} g\left( x \right)$.Ví dụ: \begin{align*} \mathop {\lim }\limits_{x \to 1} \dfrac{{{x^3} - 1}}{{x - 1}} &= \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}{{x - 1}}\\ &= \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + x + 1} \right) \\ &= 3 \end{align*}
Kĩ thuật chia:
Ví dụ: \begin{align*} \mathop {\lim }\limits_{x \to - 3} \dfrac{{{x^2} + x - 6}}{{x + 3}} &= \mathop {\lim }\limits_{x \to - 3} \dfrac{{\left( {x + 3} \right)\left( {x - 2} \right)}}{{x + 3}}\\ &= \mathop {\lim }\limits_{x \to - 3} \left( {x - 2} \right)\\ & = - 5 \end{align*}
Kĩ thuật nhân lượng liên hợp:
Ví dụ: \begin{align*} \mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {x + 1} - 1}}{x} &= \mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {\sqrt {x + 1} - 1} \right)\left( {\sqrt {x + 1} + 1} \right)}}{{x\left( {\sqrt {x + 1} + 1} \right)}}\\ &= \mathop {\lim }\limits_{x \to 0} \dfrac{x}{{x\left( {\sqrt {x + 1} + 1} \right)}}\\ &= \mathop {\lim }\limits_{x \to 0} \dfrac{1}{{\sqrt {x + 1} + 1}} \\ &= \dfrac{1}{2} \end{align*}
Định lý kẹp: Nếu $h\left( x \right) \leq f\left( x \right) \leq g\left( x \right)$ với $\forall x$ trong khoảng mở chứa $c$ (trừ tại $c$) và $\mathop {\lim }\limits_{x \to c} h\left( x \right) = L = \mathop {\lim }\limits_{x \to c} g\left( x \right)$ thì $\mathop {\lim }\limits_{x \to c} f\left( x \right) = L$.
Ví dụ: Tính giới hạn $\lim\limits_{x \to \infty} \dfrac{\sin x}{x}$.
Giải: \begin{align*} &\text{Ta có:} - 1 \leq \sin x \leq 1\\ & \Rightarrow \dfrac{{ - 1}}{x} \leq \dfrac{{\sin x}}{x} \leq \dfrac{1}{x}\\ & \Rightarrow \mathop {\lim }\limits_{x \to \infty } \dfrac{{ - 1}}{x} \leq \mathop {\lim }\limits_{x \to \infty } \dfrac{{\sin x}}{x} \leq \mathop {\lim }\limits_{x \to \infty } \dfrac{1}{x}\\ & \Rightarrow 0 \leq \mathop {\lim }\limits_{x \to \infty } \dfrac{{\sin x}}{x} \leq 0 \end{align*} Vậy $\mathop {\lim }\limits_{x \to \infty } \dfrac{{\sin x}}{x} = 0$.
Hai giới hạn lượng giác đặc biệt:
- $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1$
- $\mathop {\lim }\limits_{x \to 0} \dfrac{{1 - \cos x}}{x} = 0$
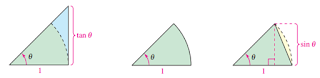
Vòng tròn lượng giác bán kính bằng 1
Tam giác lớn ($S_1$), Hình quạt ($S_2$) và Tam giác nhỏ ($S_3$)
Ta có diện tích của tam giác lớn ($S_1$), hình quạt ($S_2$) và tam giác nhỏ ($S_3$) (xem hình \ref{refhinh3}): $$\dfrac{{\tan \theta }}{2} \geq \dfrac{\theta }{2} \geq \dfrac{{\sin \theta }}{2}$$ Nhân 3 vế với $\dfrac{2}{{\sin \theta }}$, ta được: $\dfrac{1}{{\cos \theta }} \geq \dfrac{\theta }{{\sin \theta }} \geq 1$ $ \Rightarrow 1 \leq \dfrac{{\sin \theta }}{\theta } \leq \cos \theta $
Mà $\mathop {\lim }\limits_{\theta \to 0} 1 = 1$ và $\mathop {\lim }\limits_{\theta \to 0} \cos \theta = 1$ nên $\mathop {\lim }\limits_{\theta \to 0} \dfrac{{\sin \theta }}{\theta } = 1$ (định lý kẹp).
Ví dụ: \begin{align*} \mathop {\lim }\limits_{x \to 0} \dfrac{{\tan x}}{x} &= \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sin x}}{x}\dfrac{1}{{\cos x}}} \right)\\ &= \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sin x}}{x}} \right)\mathop {\lim }\limits_{x \to 0} \left( {\dfrac{1}{{\cos x}}} \right)\\ &= 1\times 1 = 1 \end{align*}
Ví dụ: $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin 4x}}{x} = 4\mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sin 4x}}{{4x}}} \right)$
Đặt $t = 4x$, do $x \to 0$ nên $t \to 0$.
Khi đó: $4\mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sin 4x}}{{4x}}} \right) = 4\mathop {\lim }\limits_{t \to 0} \left( {\dfrac{{\operatorname{sint} }}{t}} \right) = 4\times 1 = 4$ \item Kĩ thuật logarithm hóa:
Áp dụng cho các bài toán giới hạn lũy thừa ở dạng vô định (${0^0}$, ${0^\infty }$): \begin{equation} \mathop {\lim }\limits_{x \to {x_0}} {\left[ {u\left( x \right)} \right]^{v\left( x \right)}} = {e^{\mathop {\lim }\limits_{x \to {x_0}} v\left( x \right)\ln u\left( x \right)}} \end{equation} Riêng với lũy thừa ở dạng ${1^\infty }$($\mathop {\lim }\limits_{x \to {x_0}} u\left( x \right) = 1$, $\mathop {\lim }\limits_{x \to {x_0}} v\left( x \right) = \infty $), ta có: \begin{equation} \mathop {\lim }\limits_{x \to {x_0}} {\left[ {u\left( x \right)} \right]^{v\left( x \right)}} = {e^{\mathop {\lim }\limits_{x \to {x_0}} \left[ {u\left( x \right) - 1} \right]v\left( x \right)}} \end{equation} \textbf{Ví dụ:} $\mathop {\lim }\limits_{x \to 0} {\left( {1 + \tan x} \right)^{\frac{1}{{\sin x}}}} = {e^{\mathop {\lim }\limits_{x \to 0} \frac{{\tan x}}{{\sin x}}}} = {e^1} = e$
2. Tính liên tục và giới hạn một bên
2.1. Tính liên tục tại một điểm và trên một khoảng mở
Liên tục tại 1 điểm: Một hàm $f$ liên tục tại $c$ khi xảy ra các điều kiện sau:- $f(c)$ xác định.
- $\mathop {\lim }\limits_{x \to c} f\left( x \right)$ tồn tại.
- $\mathop {\lim }\limits_{x \to c} f\left( x \right) = f\left( c \right)$
Một hàm số liên tục trên khoảng mở khi hàm số liên tục tại mọi điểm trên khoảng.
2.2. Giới hạn một bên và tính liên tục trên khoảng đóng
Giới hạn bên phải: $x$ tiến về $c$ từ những giá trị lớn hơn $c$. $$\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right) = L$$Giới hạn bên phải: $x$ tiến về $c$ từ những giá trị nhỏ hơn $c$. $$\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right) = L$$
Ví dụ: Nếu $n$ là số nguyên dương chẵn, ta có: $\mathop {\lim }\limits_{x \to {0^ + }} \sqrt[n]{x} = 0$.
Ví dụ: Hàm số nguyên lớn nhất: $\left[\kern-0.15em\left[ x \right]\kern-0.15em\right] = \left\{ {\max \left( {n \in Z} \right)/n \leq x} \right\}$, ví dụ: $\left[\kern-0.15em\left[ { - 2,5} \right]\kern-0.15em\right] = - 3$, $\left[\kern-0.15em\left[ {2,5} \right]\kern-0.15em\right] = 2$. Ta có: $\mathop {\lim }\limits_{x \to {0^ - }} \left[\kern-0.15em\left[ x \right]\kern-0.15em\right] = - 1$ và $\mathop {\lim }\limits_{x \to {0^ + }} \left[\kern-0.15em\left[ x \right]\kern-0.15em\right] = 0$.
Hàm số nguyên lớn nhất $f(x)=\left[\kern-0.15em\left[ x
\right]\kern-0.15em\right] = \left\{ {\max \left( {n \in Z} \right)/n \leq x} \right\}$
Liên tục trên khoảng đóng: Một hàm số $f$ liên tục trên khoảng đóng $\left[ {a,b} \right]$ khi $f$ liên tục trên khoảng mở $\left( {a,b} \right)$ và $\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right)$ và $\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)$.
Tính chất của tính liên tục: Nếu $f$ và $g$ là các hàm số liên tục tại $x = c$ và $b$ là số thực thì các hàm số $bf\left( x \right)$, $f \pm g$, $fg$, $\dfrac{f}{g}$ ($g\left( c \right) \neq 0$) cũng liên tục tại $c$.
Tính liên tục của hàm hợp: Nếu $g$ liên tục tại $c$ và $f$ liên tục tại $g\left( c \right)$ thì $\left( {f \circ g} \right)\left( x \right) = f\left( {g\left( x \right)} \right)$ liên tục tại $c$.
Định lý giá trị trung gian: Nếu $f$ liên tục trên khoảng đóng $\left[ {a,b} \right]$, $f\left( a \right) \ne f\left( b \right)$ và $f\left( a \right) < k < f\left( b \right)$ thì có ít nhất một giá trị $c \in \left[ {a,b} \right]$ để $f\left( c \right) = k$. \end{itemize}
3. Giới hạn vô cực
Gọi $f$ là một hàm số được xác định tại mọi điểm trên vài khoảng mở chứa $c$ (trừ tại $c$). Khi đó:- $\mathop {\lim }\limits_{x \to c} f\left( x \right) = + \infty $ có nghĩa là với mỗi $M > 0$ sẽ $\exists \delta > 0$ sao cho $f\left( x \right) > M$ khi $0 < \left| {x - c} \right| < \delta $.
- $\mathop {\lim }\limits_{x \to c} f\left( x \right) = - \infty $ có nghĩa là với mỗi $N < 0$ sẽ $\exists \delta > 0$ sao cho $f\left( x \right) < N$ khi $0 < \left| {x - c} \right| < \delta $.
4. Vô cùng bé (Infinitesimal)
4.1. Định nghĩa
Hai hàm số $f(x)$ và $g(x)$ được gọi là hai vô cùng bé (VCB) khi $x$ tiến về $x_0$ nếu $$\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 0$$ Ta nói $f(x)$ và $g(x)$ là hai VCB tương đương nếu $$\mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right)}}{{g\left( x \right)}} = 1$$ Khi đó, ta viết: $f\left( x \right)\sim g\left( x \right)$.4.2. Một số cặp VCB thường gặp
Nếu $\mathop {\lim }\limits_{x \to {x_0}} u\left( x \right) = 0$ thì ta có các cặp VCB:$\sin u\left( x \right)\sim u\left( x \right)$ \item $\arcsin u\left( x \right)\sim u\left( x \right)$ \item $\tan u\left( x \right)\sim u\left( x \right)$ \item $\arctan u\left( x \right)\sim u\left( x \right)$
${e^{u\left( x \right)}} - 1\sim u\left( x \right)$ \item $\ln \left[ {1 + u\left( x \right)} \right]\sim u\left( x \right)$
${\left[ {1 + u\left( x \right)} \right]^{\text{n}}} - 1\sim \text{n}u\left( x \right)$
$1 - \cos u\left( x \right)\sim\dfrac{{{{\left[ {u\left( x \right)} \right]}^2}}}{2}$
Ví dụ: Tính $\mathop {\lim }\limits_{x \to 2} \dfrac{{\sin \left( {2 - x} \right)}}{{4 - {x^2}}}$.
Giải:
Ta có: \begin{align*} L = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sin \left( {2 - x} \right)}}{{4 - {x^2}}} &= \mathop {\lim }\limits_{x \to 2} \dfrac{{\sin \left( {2 - x} \right)}}{{\left( {2 - x} \right)\left( {2 + x} \right)}} \\ &= \mathop {\lim }\limits_{x \to 2} \dfrac{{\sin \left( {2 - x} \right)}}{{\left( {2 - x} \right)}}\mathop {\lim }\limits_{x \to 2} \left( {2 + x} \right) \\ &= 4\mathop {\lim }\limits_{x \to 2} \dfrac{{\sin \left( {2 - x} \right)}}{{2 - x}} \end{align*} Đặt $t = 2 - x$. Khi $x \to 2$ thì $t \to 0$, ta có: $L = 4\mathop {\lim }\limits_{t \to 0} \dfrac{{\sin t}}{t}$.
Thay cặp VCB: $\sin t\sim t$, ta được: $L = 4\mathop {\lim }\limits_{t \to 0} \dfrac{t}{t} = 4$
Ví dụ: Tính $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin \left( {2 + x} \right)}}{{2 + x}}$
Giải:
Không được thay cặp VCB: $\sin \left( {2 + x} \right)\sim \left( {2 + x} \right)$ vì $\mathop {\lim }\limits_{x \to 0} \sin \left( {2 + x} \right) \neq 0$.\\ Ta có: $L = \mathop {\lim }\limits_{x \to 0} \dfrac{{\sin \left( {2 + x} \right)}}{{2 + x}} = \dfrac{{\sin 2}}{2}$
Ví dụ: Tính $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x - x}}{{x + {x^3}}}$.
Giải:
Thay các cặp VCB tương đương: $\left( {\sin x - x} \right)\sim x - x = 0$, trong khi đó: $\mathop {\lim }\limits_{x \to 0} \left( {x + {x^3}} \right) = 0$.
Sau khi thay các cặp VCB, ta vẫn còn dạng vô định 0/0 nên không sử dụng VCB để tính giới hạn này.
4.3. So sánh hai VCB
Gọi $f(x)$ và $g(x)$ là 2 VCB khi $x \to {x_0}$ và $\exists \mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right)}}{{g\left( x \right)}} = L$, khi đó:- Nếu $L \neq 0$ và $L \neq \infty $ thì ta nói $f(x)$ và $g(x)$ là 2 VCB “cùng cấp”.
- Nếu $L=0$ thì ta nói $f(x)$ là VCB “cấp cao hơn” $g(x)$ và $f\left( x \right) + g\left( x \right)\sim g\left( x \right)$
- Nếu $L = \infty $ thì ta nói $g(x)$ là VCB “cấp cao hơn” $f(x)$ và $f\left( x \right) + g\left( x \right)\sim f\left( x \right)$.
Ví dụ: Tính $\mathop {\lim }\limits_{x \to 0} \dfrac{{1 - \cos x + \sin x}}{x}$
Giải:
Ta thay các cặp VCB tương đương: $1 - \cos x\sim \dfrac{{{x^2}}}{2}$, $\sin x\sim x$.
Dễ thấy: $\mathop {\lim }\limits_{x \to 0} \dfrac{{1 - \cos x}}{{\sin x}} = \mathop {\lim }\limits_{x \to 0} \dfrac{{{x^2}}}{{2x}} = 0$
Do đó: $1 - \cos x$ là VCB cấp cao hơn $\sin x$ và $1 - \cos x + \sin x\sim x$
Như vậy: $L = \mathop {\lim }\limits_{x \to 0} \dfrac{{1 - \cos x + \sin x}}{x} = \mathop {\lim }\limits_{x \to 0} \dfrac{x}{x} = 1$.
5. Vô cùng lớn (Infinite)
$f(x)$ được gọi là vô cùng lớn (VCL) khi $\mathop {\lim }\limits_{x \to {x_0}} \left| {f\left( x \right)} \right| = + \infty $.Các tính chất ngược lại VCB.
Chú ý: Nếu $p(x)$ và $q(x)$ là các đa thức cùng bậc, khi đó: \begin{equation} \lim\limits_{x \to \infty} \dfrac{p(x)}{q(x)} = \dfrac{\text{hệ số của số hạng bậc cao nhất của } p(x)}{\text{hệ số của số hạng bậc cao nhất của } q(x)} \end{equation}
Ví dụ: Ta có: $\lim\limits_{x \to \infty} \dfrac{1992+2x+17x^2}{1997+9x+18x^2} =\dfrac{17}{18}$
Bài tập
Áp dụng cho các bài từ 1 - 12. Tính giới hạn dãy số1. $\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {n + 1} - \sqrt n } \right)$
2. $\mathop {\lim }\limits_{n \to + \infty } \dfrac{{n\sin n}}{{{n^2} + 1}}$
3. $\mathop {\lim }\limits_{n \to + \infty } \dfrac{{{2^{n + 1}} + {3^{n + 1}}}}{{{2^n} + {3^n}}}$
4. $\mathop {\lim }\limits_{n \to + \infty } \root n \of {{a^n} + {b^n} + {c^n}}$ với $a,b,c > 0$
5. $\mathop {\lim }\limits_{n \to + \infty } n \sin \dfrac{\pi }{n}$
6. $\mathop {\lim }\limits_{n \to + \infty } \sin \left( {\pi \sqrt {{n^2} + 1} } \right)$
7. $\mathop {\lim }\limits_{n \to + \infty } \left| {\sin \left( {\pi \sqrt {{n^2} + n + 1} } \right)} \right|$
8. $\mathop {\lim }\limits_{n \to + \infty } \dfrac{{\sin \pi n + 4\root 3 \of n }}{{\root 3 \of {n + 1} }}$
9. $\mathop {\lim }\limits_{n \to + \infty } \dfrac{{1 + a + {a^2} + \cdots+ {a^n}}}{{1 + b + {b^2} + \cdots + {b^n}}}$ với $\left| a \right|,\left| b \right| < 1$
10. $\mathop {\lim }\limits_{n \to + \infty } \dfrac{{n\sqrt {1 + 3 + \cdots + (2n - 1)} }}{{2{n^2} + n + 1}}$
11. $\mathop {\lim }\limits_{n \to + \infty } \sqrt 2 \root 4 \of 2 \root 8 \of 2 \cdots \root {{2^n}} \of 2 $
12. $\mathop {\lim }\limits_{n \to + \infty } \dfrac{{{1^2} + {2^2} + \cdots + {n^2}}}{{{n^3}}}$
Áp dụng cho các bài từ 13 - 42. Tính giới hạn hàm số bằng các kĩ thuật tính giới hạn:
13. $\mathop {\lim }\limits_{x \to 4} \dfrac{{\sqrt {1 + 2x} - 3}}{{\sqrt x - 2}}$
14. $\mathop {\lim }\limits_{x \to 1} \dfrac{{\root m \of x - 1}}{{\root n \of x - 1}}$
15. $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {x + \sqrt {x + \sqrt x } } - \sqrt x } \right)$
16. $\mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {1 - \sqrt x } \right)\left( {1 - \root 3 \of x } \right)\cdots\left( {1 - \root n \of x } \right)}}{{{{\left( {1 - x} \right)}^{n - 1}}}}$
17. $\mathop {\lim }\limits_{x \to + \infty } \dfrac{{{{\left( {x - \sqrt {{x^2} - 1} } \right)}^n} + {{\left( {x + \sqrt {{x^2} - 1} } \right)}^n}}}{{{x^n}}}$
18. $\mathop {\lim }\limits_{x \to + \infty } \sqrt {(x + {a_1})(x + {a_2})} - x$
19. $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin 5x}}{{\tan 8x}}$
20. $\mathop {\lim }\limits_{x \to 0} \left( {\dfrac{1}{{\sin x}} - \cot x} \right)$
21. $\mathop {\lim }\limits_{x \to + \infty } x\sin \dfrac{1}{x}$
22. $\mathop {\lim }\limits_{x \to 5} \left( {5 - x} \right)\tan \dfrac{{\pi x}}{{10}}$
23. $\mathop {\lim }\limits_{x \to 0} \dfrac{{1 - \sqrt {\cos x} }}{{{x^2}}}$
24. $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + \sin x} - \sqrt {1 - \sin x} }}{x}$
25. $\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \cos x}}{{{x^2}}}$
26. $\mathop {\lim }\limits_{x \to 0} \dfrac{{\root 3 \of {\cos x } - \sqrt {\cos x} }}{{{x^2}}}$
27. $\mathop {\lim }\limits_{x \to 0} \dfrac{{{x^2}}}{{\sqrt {1 + x\sin 3x} - \sqrt {\cos 2x} }}$
28. $\mathop {\lim }\limits_{x \to 0} \dfrac{{1 - \cos x\cos 2x\cos 3x}}{{{x^2}}}$
29. $\mathop {\lim }\limits_{x \to 0} \dfrac{{1 + \sin x - \cos x}}{{1 + \sin \left( {ax} \right) - \cos \left( {ax} \right)}}$ với $a \neq 0$
30. $\mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt {1 + x + {x^2}} - \sqrt {7 + 2x - {x^2}} }}{{{x^2} - 2x}}$
31. $\mathop {\lim }\limits_{x \to 0} \dfrac{{{5^x} - {4^x}}}{{{x^2} + x}}$
32. $\mathop {\lim }\limits_{x \to 1} \dfrac{{{x^x} - 1}}{{x\ln x}}$
33. $\mathop {\lim }\limits_{x \to + \infty } {\left( {\dfrac{{x + 2}}{{x - 3}}} \right)^{3x + 4}}$
34. $\mathop {\lim }\limits_{x \to 0} {(\cos x)^{\frac{1}{{{x^2}}}}}$
35. $\mathop {\lim }\limits_{x \to 0} {(\cos x)^{\frac{1}{{\sin x}}}}$
36. $\mathop {\lim }\limits_{x \to 0} {(1 + \sin x)^{\frac{1}{x}}}$
37. $\mathop {\lim }\limits_{x \to 0} {\left( {\dfrac{{1 + \tan x}}{{1 + \sin x}}} \right)^{\frac{1}{{\sin x}}}}$
38. $\mathop {\lim }\limits_{x \to \infty } \dfrac{{{2^x} + 3}}{{{2^x} - 3}}$
39. $\mathop {\lim }\limits_{x \to {1^ + }} \left( {1 - x} \right)\sqrt {\dfrac{{x + 5}}{{{x^2} + 2x - 3}}} $
40. $\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{\ln (1 + {e^x})}}{x}$
41. $\mathop {\lim }\limits_{x \to {1^ \pm }} {2^{\frac{1}{{x - 1}}}}$
42. $\mathop {\lim }\limits_{x \to {\pi ^ + }} \dfrac{{\sqrt {1 + \cos x} }}{{\sin x}}$
43. Để thoát khỏi trường trọng lực của Trái Đất, một tên lửa được phóng lên với vận tốc ban đầu hay còn gọi là “vận tốc thoát”. Tên lửa được phóng từ mặt đất của Trái Đất với vận tốc $v$ (tính theo dặm/s) được cho bởi \begin{align*} v = \sqrt {\dfrac{{2GM}}{r} + v_0^2 - \dfrac{{2GM}}{R}} \approx \sqrt {\dfrac{{192000}}{r} + v_0^2 - 48} \end{align*} Trong đó $v_0$ là vận tốc ban đầu, là khoảng cách từ tên lửa đến tâm Trái Đất, $G$ là hằng số hấp dẫn,$M$ là khối lượng của Trái Đất và $R$ là bán kính của Trái Đất (xấp xỉ 4000 dặm).
Cho biết 1 dặm $\approx$ 1,6 km.
a. Tìm giá trị vận tốc $v_0$ biết rằng khi tên lửa ra xa vô cực thì vận tốc $v$ tiến về 0. Giá trị $v_0$ là vận tốc thoát cho Trái Đất.
b. Một tên lửa được phóng từ bề mặt của Mặt Trăng có vận tốc $v$ (tính theo dặm/s) được cho bởi \begin{align*} v = \sqrt {\dfrac{{1920}}{r} + v_0^2 - 2.17} \end{align*} Xác định vận tốc thoát cho Mặt Trăng. c. Một tên lửa được phóng từ bề mặt của một hành tinh có vận tốc $v$ (tính theo dặm/s) được cho bởi \begin{align*} v = \sqrt {\dfrac{{10600}}{r} + v_0^2 - 6.99} \end{align*} Tìm vận tốc thoát cho hành tinh này. Khối lượng của hành tinh này lớn hơn hay nhỏ hơn khối lượng Trái Đất? (Giả sử rằng mật độ vật chất trung bình của hành tinh và Trái Đất là như nhau).
Áp dụng cho các bài từ 44 - 54. Tính giới hạn hàm số bằng cách sử dụng các đại lượng VCB tương đương:
44. $\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + 2x\sin x} \right)}}{{{{\tan }^2}x}}$
45. $\mathop {\lim }\limits_{x \to 0} \dfrac{{\root 3 \of {8 + 3x} - 2}}{{\root 4 \of {16 + 5x} - 2}}$
46. $\mathop {\lim }\limits_{x \to 0} \dfrac{{{{\sin }^2}3x}}{{{{\ln }^2}(1 - 2x)}}$
47. $\mathop {\lim }\limits_{x \to 1} \dfrac{{\sin ({e^{x - 1}} - 1)}}{{\ln x}}$
48. $\mathop {\lim }\limits_{x \to {{\frac{\pi }{2}}^ + }} \dfrac{{\sqrt {1 + \cos 2x} }}{{\sqrt \pi - \sqrt {2x} }}$
49. $\mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {1 - {e^x}} \right)\left( {1 - \cos x} \right)}}{{{x^3} + {{\sin }^4}x}}$
50. $\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {\cos x} \right)}}{{\ln \left( {1 + {x^2}} \right)}}$
51. $\mathop {\lim }\limits_{x \to 0} \dfrac{{\arcsin \dfrac{x}{{\sqrt {1 - {x^2}} }}}}{{\ln \left( {1 - x} \right)}}$
52. $\mathop {\lim }\limits_{x \to \frac{1}{2}} \dfrac{{4{x^2} - 1}}{{\arcsin \left( {1 - 2x} \right)}}$
53. $\mathop {\lim }\limits_{x \to 0} \dfrac{{\root 3 \of {1 + {{\tan }^2}x} - \root 3 \of {1 - {{\arctan }^2}x} }}{{x + \root 3 \of {{x^2}} }}$
54. $\mathop {\lim }\limits_{x \to 0} {\left( {\dfrac{{1 + \sin x\cos 2x}}{{1 + \sin x\cos 3x}}} \right)^{{{\cot }^3}x}}$
Áp dụng cho các bài từ 55 - 62. So sánh VCB $\alpha(x)$ và $\beta(x)$ khi $x \to 0$, chúng có phải là VCB tương đương không?
55. $\alpha \left( x \right) = x{\sin ^2}x$ và $\beta \left( x \right) = {x^2}\sin x$
56. $\alpha \left( x \right) = 1 - {\cos ^3}x$ và $\beta \left( x \right) = x\sin x$
57. $\alpha \left( x \right) = \sin x - \tan x$ và $\beta \left( x \right) = 1 - \cos x$
58. $\alpha \left( x \right) = {a^x} - 1$ và $\beta \left( x \right) = x\ln a$ với $a>0$.
59. $\alpha \left( x \right) = \cos x - \cos 2x$ và $\beta \left( x \right) = {x^{\frac{3}{2}}}$ với $x>0$.
60. $\alpha \left( x \right) = {e^{2x}} - {e^x}$ và $\beta \left( x \right) = \sin 2x - x$
61. $\alpha \left( x \right) = \sqrt {{x^3} + {{\sin }^2}x} $ và $\beta \left( x \right) = x$
62. $\alpha \left( x \right) = x\sin \dfrac{1}{x}$ và $\beta \left( x \right) = x$.
Áp dụng cho các bài từ 63 và 64. Xét tính liên tục của hàm số
63. $f(x) = \left\{\begin{matrix} \dfrac{\sin x}{|x|} &, x\neq 0 \\ 1 &, x=0 \end{matrix} \right. $
64. $f(x) = \left\{\begin{matrix} x^2 \sin \dfrac{1}{|x|} &, x\neq 0 \\ 0 &, x=0 \end{matrix} \right.$
65. Xác định các giá trị của hằng số $a$ sao cho hàm sau liên tục tại mọi điểm trên tập số thực. \begin{align*} f(x) = \left\{\begin{matrix} \dfrac{a x}{\tan x} &, x \geq 0 \\\\ a^2 - 2 &, x



No comments:
Post a Comment